There is an increasing concern with measuring and comparing the efficiency of organisational units such as local authority departments, schools, hospitals, shops, bank branches and similar instances where there is a relatively homogeneous set of units.
The usual measure of efficiency, i.e.:
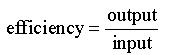
is often inadequate due to the existence of multiple inputs and outputs related to different resources, activities and environmental factors. This problem can be illustrated for depots of a large retailing organisation which distributes goods to supermarkets. In this case the inputs for an efficiency measure are taken to be the value of the stock and the recurrent costs mainly in the form of wages, as those are resources supporting the operation of the depots. Stock is reasonably an input to an efficiency measure as an efficient depot will attempt to give a good service at lower stock levels, saving on capital and space. The outputs correspond to activities of the depots and are measured by the number of issues representing deliveries to supermarkets, the number of receipts in bulk from suppliers, and the number of requisitions on suppliers where they are out of stock or approaching stock out. (A further possible output would be a measure of the service level). The data on these measures is shown in the following table.
| STOCK(£M) | WAGES(£100,000’S) | ISSUES(00’S) | RECEIPTS(000’S) | REQS(000’S) | |
| Depot 1 | 3 | 5 | 40 | 55 | 30 |
| Depot 2 | 2.5 | 4.5 | 45 | 50 | 40 |
| Depot 3 | 4 | 6 | 55 | 45 | 30 |
| Depot 4 | 6 | 7 | 48 | 20 | 60 |
| Depot S | 2.3 | 3.5 | 28 | 50 | 25 |
| Depot 6 | 4 | 6.5 | 48 | 20 | 65 |
| Depot 7 | 7 | 10 | 80 | 65 | 57 |
| Depot 8 | 4.4 | 6.4 | 25 | 48 | 30 |
| Depot 9 | 3 | 5 | 45 | 64 | 42 |
| Depot 10 | 5 | 7 | 70 | 65 | 48 |
| Depot 11 | 5 | 7 | 45 | 65 | 40 |
| Depot12 | 2 | 4 | 45 | 40 | 44 |
| Depot13 | 5 | 7 | 65 | 25 | 35 |
| Depot14 | 4 | 4 | 38 | 18 | 64 |
| Depot15 | 2 | 3 | 20 | 50 | 15 |
| Depot16 | 3 | 6 | 38 | 20 | 60 |
| Depot17 | 7 | 11 | 68 | 64 | 54 |
| Depot18 | 4 | 6 | 25 | 38 | 20 |
| Depot19 | 3 | 4 | 45 | 67 | 32 |
| Depot20 | 5 | 6 | 57 | 60 | 40 |
With two inputs and three outputs the difficulty of comparing the efficiency of depots becomes apparent. Some statements concerning the relative efficiency of depots can be made, for example comparing depots 10 and 11. These both have the same stock levels and the same costs but depot 10 has activity levels which are all as great or greater than those of depot 11. Clearly if these inputs and outputs are representative then depot 10 is more efficient than depot 11. However the majority of comparisons are difficult to make. For example comparing depots 14 and 15, depot 14 has higher inputs and has higher outputs on two measures but lower on one measure. Here different patterns of activity levels are supported by different amounts of resources making efficiency comparisons difficult and this is generally the case.
A formula for relative efficiency incorporating multiple inputs and outputs is introduced now, and the DEA model which allows relative efficiency measures to be determined is developed. This is followed by a discussion of the information made available by solving the model and some issues of practical concern in applying the technique.














